Bachelor-Thesis - Reinforcement Learning in der Praxis

Reinforcement Learning in der Praxis: Anwendung von Deep Q-Learning in dynamischen Umgebungen am Beispiel von Tetris. Ziel der Bachelor-Thesis war es den Reinforcement Learning Algorithmus Deep Q-Learning im Computerspiel Tetris anzuwenden, um einen möglichst hohen Highscore zu erzielen.

---

Inhaltsverzeichnis

1. Einleitung und theoretische Grundlage
2. Anwendung von Deep Q-Learning auf Tetris
   1. Erster Lösungsansatz
   2. Zweiter Lösungsansatz
3. Training und Auswertung
4. Fazit und Ausblick

Einleitung und theoretische Grundlage

Diese Abschlussarbeit beschäftigt sich mit der Entwicklung einer künstlichen Intelligenz, die selbstständig das klassische Videospiel Tetris spielen kann. Das Ziel besteht darin, mithilfe des Deep Q-Learning Algorithmus eine KI zu trainieren, die durch eigenständiges Ausprobieren und Lernen aus Fehlern eine erfolgreiche Spielstrategie entwickelt.

Tetris eignet sich besonders gut für diese Art des maschinellen Lernens, da Videospiele eine risikofreie Experimentierumgebung bieten. Anders als bei kritischen Anwendungen wie autonomem Fahren oder Aktienhandel können hier beliebig viele Versuche unternommen werden, ohne negative Konsequenzen zu verursachen. Zusätzlich lassen sich Spiele beliebig oft zurücksetzen und in beschleunigter Geschwindigkeit abspielen, was der KI optimale Lernbedingungen ermöglicht.

Die methodische Grundlage bildet der Deep Q-Learning Algorithmus aus dem Bereich des Reinforcement Learning. Dieser Ansatz ersetzt traditionelle Q-Tables durch neuronale Netze, wodurch auch komplexere Spielsituationen mit einer großen Anzahl möglicher Zustände effizient verarbeitet werden können. Das System nutzt Techniken wie Experience Replay und die Epsilon-Greedy Strategy, um ein ausgewogenes Verhältnis zwischen dem Erkunden neuer Strategien und der Anwendung bereits erlernten Wissens zu gewährleisten.

Für die praktische Umsetzung wurde eine vollständige Tetris-Implementierung nach den offiziellen Tetris Guidelines entwickelt, die ein 10x20 Spielfeld mit allen sieben Tetromino-Typen umfasst. Aufbauend auf dieser Basis werden zwei verschiedene Lösungsansätze verfolgt: eine Standard-Implementation des Algorithmus und eine optimierte Version, die speziell an die Tetris-Problemstellung angepasst wurde. Verschiedene KI-Modelle analysieren dabei unterschiedliche Eigenschaften des Spielfelds, um deren Aussagekraft und die resultierenden Spielstile systematisch zu vergleichen.

Als ultimativer Erfolgsnachweis für die entwickelte KI gilt das Erreichen von einer Million Punkten, was eine nachhaltige und verlustfreie Spielweise über einen längeren Zeitraum demonstriert und beweist, dass das System die Komplexität von Tetris erfolgreich gemeistert hat.

Anwendung von Deep Q-Learning auf Tetris

Die praktische Umsetzung basierte auf einer bestehenden JavaScript-Tetris-Implementierung, die zunächst nach Python portiert und anschließend als Grundlage für das Deep Q-Learning System verwendet wurde. Der Entwicklungsprozess gliederte sich in zwei aufeinanderfolgende Lösungsansätze, wobei der erste Versuch aufgrund ausbleibender Lernerfolge scheiterte und grundlegende Probleme im theoretischen Modell offenlegte.

Diese Erkenntnisse führten zum zweiten Lösungsansatz, der weitreichende Anpassungen des ursprünglichen Algorithmus erforderte. Die vorgenommenen Modifikationen wichen so stark vom theoretischen Grundmodell ab, dass dieses nicht mehr in seiner ursprünglichen Form anwendbar war. Dieser pragmatische Ansatz erwies sich jedoch als erfolgreich und ermöglichte umfangreiche Experimente mit verschiedenen KI-Modellen, um die Relevanz unterschiedlicher Spielfeld-Eigenschaften für die Bewertung von Spielsituationen zu analysieren.

Ein zentraler Baustein beider Lösungsansätze war die strategische Vereinfachung der Umgebungsdarstellung durch Feature-Engineering. Anstatt das komplette Spielfeld als Matrix zu übertragen, wurden spezifische Gütekriterien entwickelt, die relevante Informationen über die aktuelle Spielsituation komprimiert wiedergeben. Diese Abstraktion sollte der KI dabei helfen, verwandte Spielsituationen zu erkennen und erlerntes Wissen auf ähnliche Szenarien zu übertragen.

Die entwickelten Features umfassen die Höhe der einzelnen Säulen, welche die Bedrohungslage aus der Vogelperspektive widerspiegelt, da hohe Säulen sowohl Schwierigkeiten beim Manövrieren als auch Platzmangel für Rotationen verursachen. Das Bumpiness-Feature misst die Unebenheit der Spielfeld-Oberfläche durch Summierung der absoluten Höhenunterschiede benachbarter Säulen und fördert einen ausgewogenen Spielstil, kann aber bei Übergewichtung zu suboptimalen Brückenbildungen führen. Die Anzahl der Löcher quantifiziert unzugängliche freie Felder unterhalb bereits platzierter Blöcke, was als kritisches Bewertungskriterium gilt, da Löcher das Komplettieren von Reihen erheblich erschweren.

Diese Feature-basierte Abstraktion erwies sich der binären Matrixdarstellung als deutlich überlegen, da sie semantisch bedeutsame Informationen extrahiert und der KI ermöglicht, von strukturell ähnlichen Spielsituationen zu lernen. Während eine binäre Kodierung jeden Spielzustand als einzigartig behandelt, erkennt die Feature-Abstraktion die zugrundeliegenden Muster und Strategien, die für erfolgreiches Tetris-Spiel entscheidend sind.

Erster Lösungsansatz

Der erste Lösungsansatz orientierte sich strikt am theoretischen Deep Q-Learning Modell und simulierte die Interaktion eines menschlichen Spielers mit einem Tetris-Spielautomaten. Dabei entsprach jeder Zeitschritt einem einzelnen Tastendruck, womit die verfügbaren Aktionen auf die elementaren Befehle Left, Right, Rotate, Hold, Soft Drop und Hard Drop beschränkt wurden. Diese Herangehensweise sollte eine möglichst direkte Übertragung des theoretischen Frameworks auf die Tetris-Umgebung ermöglichen.

Die Systemarchitektur folgte den klassischen Deep Q-Learning Prinzipien mit einem definierten Action Space von sechs atomaren Aktionen und einem Observation Space, der die entwickelten Features wie Score, Anzahl der Löcher, Bumpiness und die Höhen aller Spielfeldsäulen umfasste. Das neuronale Netz wurde entsprechend dimensioniert, wobei jedes State-Feature einem Input-Neuron und jede mögliche Aktion einem Output-Neuron entsprach.

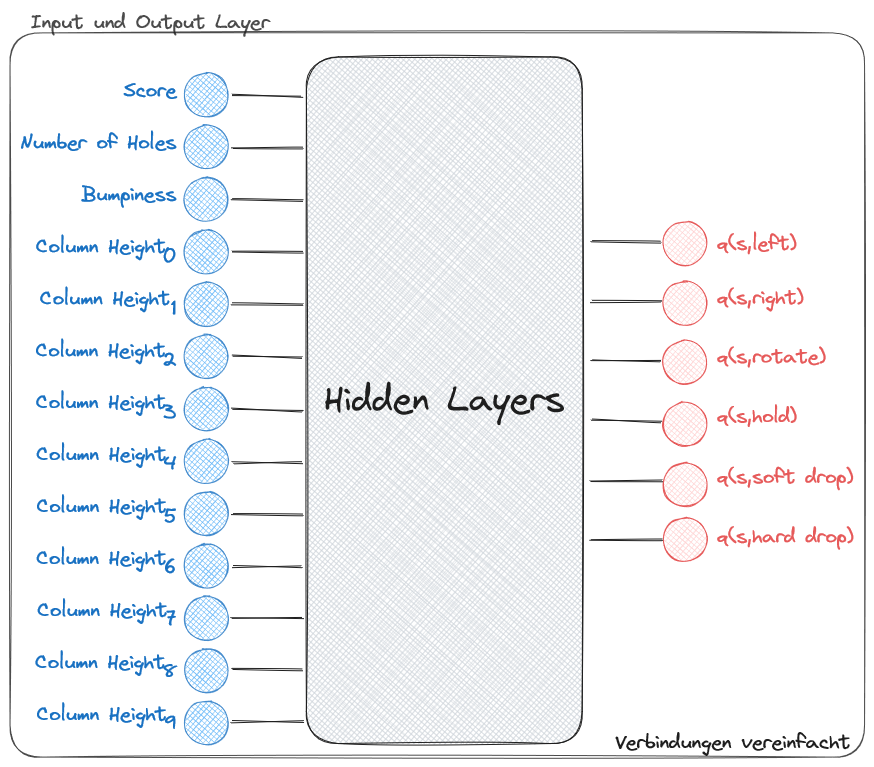
Trotz der theoretisch korrekten Implementierung offenbarte das Training fundamentale Schwächen dieses Ansatzes. Das erste Problem lag in der Vielzahl trivialer Schritte, da sich der Spielzustand ausschließlich beim Ablegen eines Tetrominos änderte, während Bewegungs- und Rotationsaktionen bis zu diesem Punkt keine messbaren Auswirkungen auf State oder Belohnung hatten. Dadurch sammelte der Agent überwiegend nutzlose Erfahrungen, aus denen kein zielführendes Wissen extrahiert werden konnte.

Ein weiteres kritisches Problem entstanden durch falsche Kausalitätsschlüsse, da der Agent Zustandsänderungen und Belohnungen ausschließlich mit den Aktionen Soft Drop und Hard Drop verknüpfte, obwohl horizontale Bewegungen und Rotationen für strategisch optimale Positionierungen unverzichtbar sind. Diese Verzerrung führte dazu, dass der Agent die Bedeutung der vorbereitenden Aktionen systematisch unterschätzte.

Zusätzlich erschwerten die unterschiedlich starken Auswirkungen der verfügbaren Aktionen das Lernen erheblich. Während Bewegungs- und Rotationsbefehle reversibel und ohne direkte Konsequenzen waren, führten Hard Drop und Hold zu sofortigen, irreversiblen Veränderungen und beeinflussten die Exploration negativ, indem sie Tetrominos kontinuierlich zur Spielfeldmitte zurückführten.

Diese strukturellen Probleme manifestierten sich im Training durch ein charakteristisches Fehlverhalten: Mit abnehmendem Epsilon begann der Agent systematisch, Tetrominos zentral abzulegen, was zu extrem kurzen Partien ohne jeden Line Clear führte. Da sich bei der zufälligen Exploration Links- und Rechtsbewegungen statistisch aufhoben, entstanden hohe zentrale Türme, die das Spiel beendeten, bevor der Agent die positive Erfahrung erfolgreicher Reihenräumungen machen konnte. Dieses Problem veranschaulicht ein fundamentales Prinzip des Reinforcement Learning: Gewünschte Verhaltensweisen müssen durch zufällige Exploration häufig genug erreicht werden, um langfristig verstärkt zu werden. Der erste Lösungsansatz scheiterte letztendlich daran, dass er den Agenten dazu verleitete, Navigation, statt strategischer Platzierung zu erlernen, obwohl letztere für erfolgreiches Tetris-Spiel entscheidend ist.

Zweiter Lösungsansatz

Der zweite Lösungsansatz adressierte die fundamentalen Schwächen des ersten Versuchs durch eine grundlegende Neukonzeption des Aktionsraums. Anstatt einzelne Tastendrücke zu simulieren, wurde der Fokus auf die strategische Entscheidung verlagert, wo ein Tetromino optimal platziert werden sollte. Diese Herangehensweise orientiert sich am natürlichen menschlichen Spielverhalten, bei dem Spieler zunächst ideale Ablagepositionen identifizieren, ohne sich primär mit der Navigation dorthin zu beschäftigen.

Die konzeptionelle Änderung führte zu einer kompletten Neudefinition des Zeitschritts: Ein Time Step entsprach nun einem vollständig abgelegten Tetromino anstelle einer einzelnen Bewegung. Dadurch wurde der Action Space von den statischen sechs Grundbefehlen auf eine dynamische Menge aller möglichen Endpositionen erweitert, die sich aus den verfügbaren Koordinaten und Rotationszuständen des aktuellen Tetrominos ergeben. Diese Flexibilität erforderte jedoch eine Anpassung der Deep Q-Learning Architektur, da die ursprüngliche Prämisse konstanter Aktionsanzahl verletzt wurde.

Die mathematische Lösung bestand im Wechsel von der Action-Value Function zur State-Value Function, da jede mögliche Aktion einem eindeutigen Folgezustand zugeordnet werden kann. Diese Vereinfachung ermöglichte die Reduktion des Output Layers auf ein einzelnes Neuron, dessen Wert die Güte des resultierenden Spielfeldzustands repräsentiert. Zur Implementierung wurde ein Wegfindungsalgorithmus entwickelt, der alle validen Endpositionen für den aktuellen und gehaltenen Tetromino ermittelt und diese durch das neuronale Netz bewertet.

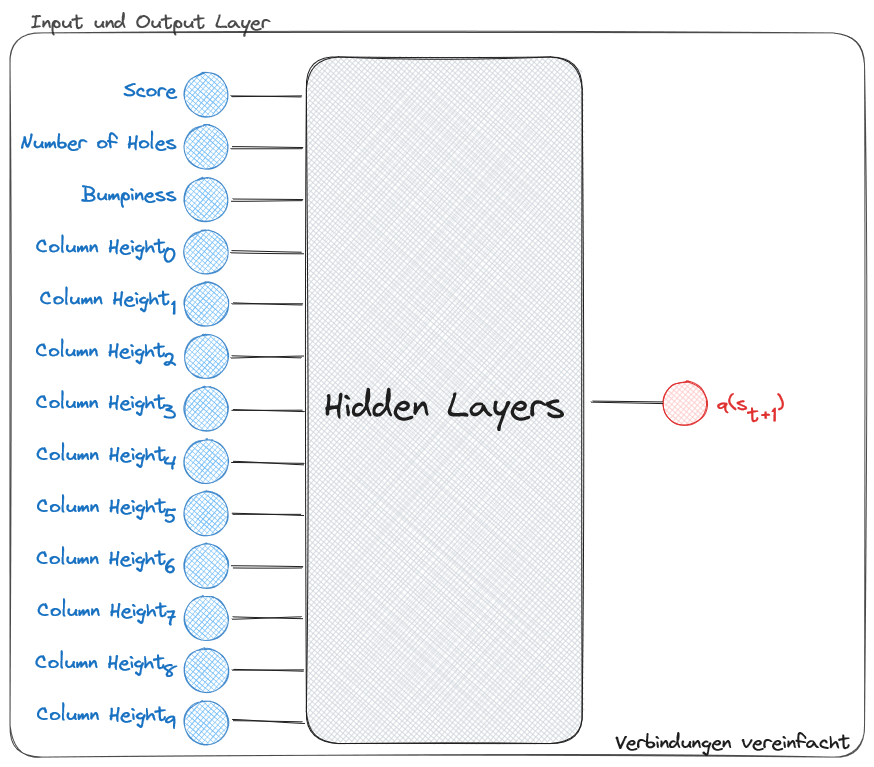
Der praktische Ablauf gestaltete sich nun folgendermaßen: In jedem Zeitschritt generiert das System alle möglichen Platzierungsoptionen, übergibt die resultierenden Spielfeldzustände an das DQN zur Bewertung und wählt bei der Exploitation die Position mit dem höchsten Q-Value aus. Anschließend wird ein Bewegungsplan erstellt, der den Tetromino zur gewählten Position navigiert.

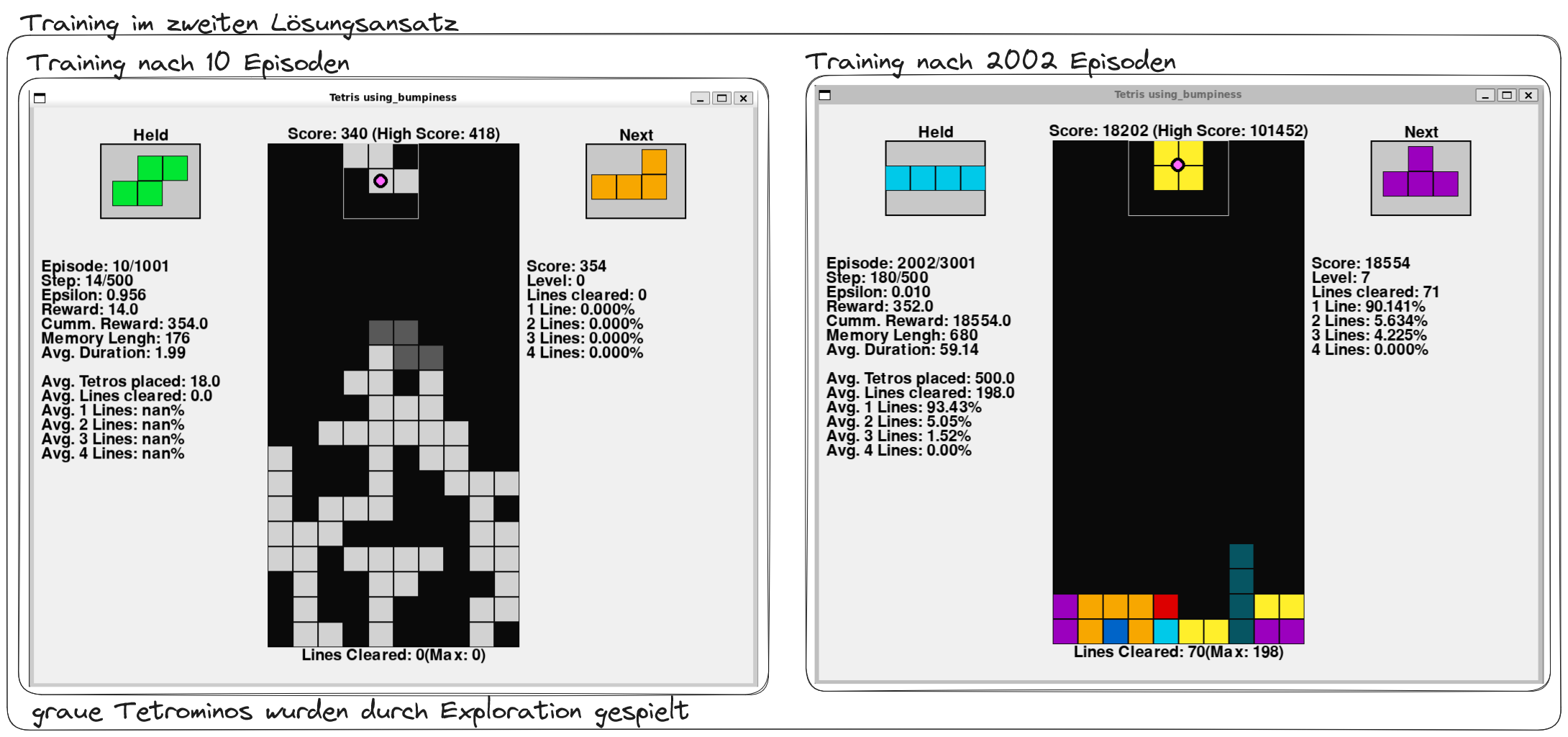
Die Trainingsergebnisse zeigten deutliche Verbesserungen gegenüber dem ersten Ansatz. Der Agent entwickelte eine ausgewogenere Platzierungsstrategie, erkundete systematisch das gesamte Spielfeld und erreichte signifikant längere Spielzeiten. Mit fortschreitendem Training und abnehmendem Epsilon kristallisierte sich ein charakteristischer Spielstil heraus: Der Agent fokussierte sich stark auf das schnelle Räumen einzelner Reihen und entwickelte eine konservative Strategie, die Lochbildung konsequent vermied. Obwohl diese Herangehensweise auf die lukrativen Tetris-Boni verzichtete, erwies sie sich als hocheffektiv für das Erreichen hoher Gesamtpunktzahlen durch nachhaltiges, risikoarmes Spiel.

Die vielversprechenden Resultate dieses Lösungsansatzes bildeten die Grundlage für weiterführende Experimente mit verschiedenen KI-Modellen, um die Relevanz unterschiedlicher Spielfeld-Features für die strategische Entscheidungsfindung zu analysieren.

Training und Auswertung

Der erfolgreiche zweite Lösungsansatz bildete die Grundlage für umfangreiche Experimente mit verschiedenen KI-Modellen, die sich in ihren beobachteten Spielfeld-Features unterschieden. Um eine unvoreingenommene Problemlösung zu gewährleisten, wurde bewusst auf Domänenwissen verzichtet und eine einfache Reward-Funktion implementiert, die ausschließlich den erzielten Punktestand als Belohnung verwendet. Zusätzlich erhielten alle Modelle eine substanzielle Bestrafung bei Spielverlust, was risikoaverse Strategien fördern sollte.

Die experimentelle Anordnung umfasste mehrere Modellvarianten mit unterschiedlichen Feature-Kombinationen, wobei der Schwerpunkt auf dem Vergleich zwischen Bumpiness und der Standardabweichung der Säulenhöhen lag. Alle Modelle erhielten das Feature “Number of Cleared Lines”, da Reihenräumung ein fundamentaler Tetris-Mechanismus ist. Ein besonderes Modell erhielt ausschließlich bei Tetris-Erfolgen Belohnungen, um dessen Auswirkungen auf die Strategieentwicklung zu analysieren.

Das Training offenbarte bemerkenswerte Muster in der Strategieentwicklung. Modelle mit Bumpiness-Feature entwickelten durchweg konservative, risikoarme Spielstile, die darauf abzielten, das Spielfeld möglichst eben zu halten und einzelne Reihen zu räumen. Diese Herangehensweise führte zu einer außergewöhnlich stabilen Leistung mit geringer Volatilität in den Punktzahlen, ermöglichte jedoch kaum Bonuspunkte durch mehrfache Reihenräumungen.

Im Gegensatz dazu entwickelte das Modell mit Standardabweichungs-Feature eine wesentlich aggressivere Strategie, die durch den Bau hoher Türme mit schmalen Zwischenräumen charakterisiert war. Diese Herangehensweise ermöglichte zwar gelegentlich spektakuläre Punktzahlen und eine höhere Rate mehrfacher Line Clears, führte jedoch auch zu einer Verlustrate von 33% selbst nach abgeschlossenem Training. Das Risiko-Ertrags-Verhältnis erwies sich als problematisch, da das Modell nicht genügend Voraussicht entwickelte, um die geschaffenen Lücken systematisch zu nutzen.

Eine überraschende Erkenntnis lieferte das Modell, das ausschließlich für Tetris-Erfolge belohnt wurde: Trotz der extrem seltenen positiven Verstärkung entwickelte es ein nahezu identisches Verhalten wie die anderen Bumpiness-Modelle. Dies deutet darauf hin, dass die negative Verstärkung bei Spielverlust einen dominierenden Einfluss auf die Strategieentwicklung hatte und konservative Ansätze begünstigte.

Die quantitative Auswertung bestätigte diese Beobachtungen eindrucksvoll. Nach etwa 1000 Trainingsepisoden erreichten alle Bumpiness-Modelle eine Plateau-Phase mit konsistenten Scores zwischen 100.000 und 101.000 Punkten bei nahezu 100%iger Erfolgsrate beim Ablegen aller 500 erlaubten Tetrominos. Ihre Tetris-Rate lag im Promillebereich, während über 93% ihrer Reihenräumungen einzelne Lines betrafen.

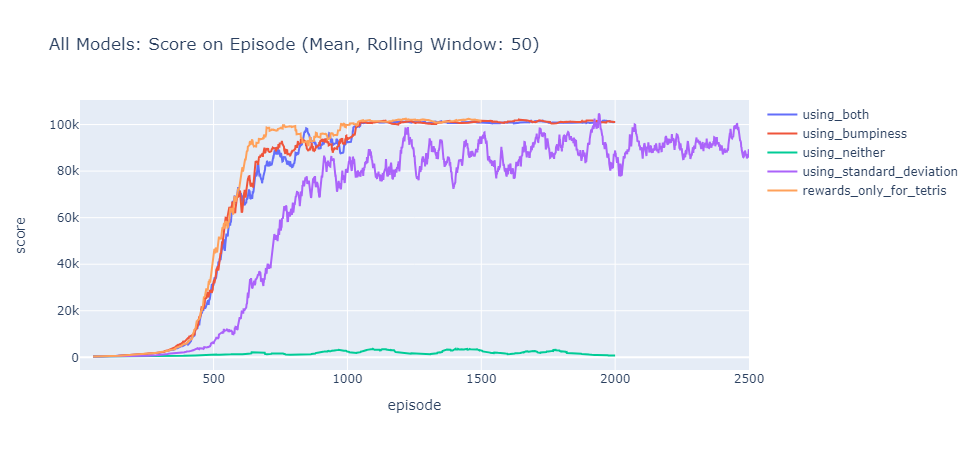
Der abschließende direkte Vergleich unter optimalen Bedingungen (Epsilon = 0) unterstrich die Überlegenheit der konservativen Strategien für das definierte Ziel von einer Million Punkten. Obwohl das Standardabweichungs-Modell initial einen Vorsprung durch effizienteren Punkteerwerb aufbaute, scheiterte es bei 74.052 Punkten am inhärenten Risiko seiner Strategie. Die Bumpiness-Modelle erreichten das Millionen-Punkte-Ziel nahezu gleichzeitig, womit sich kein eindeutiger Sieger ermitteln ließ.

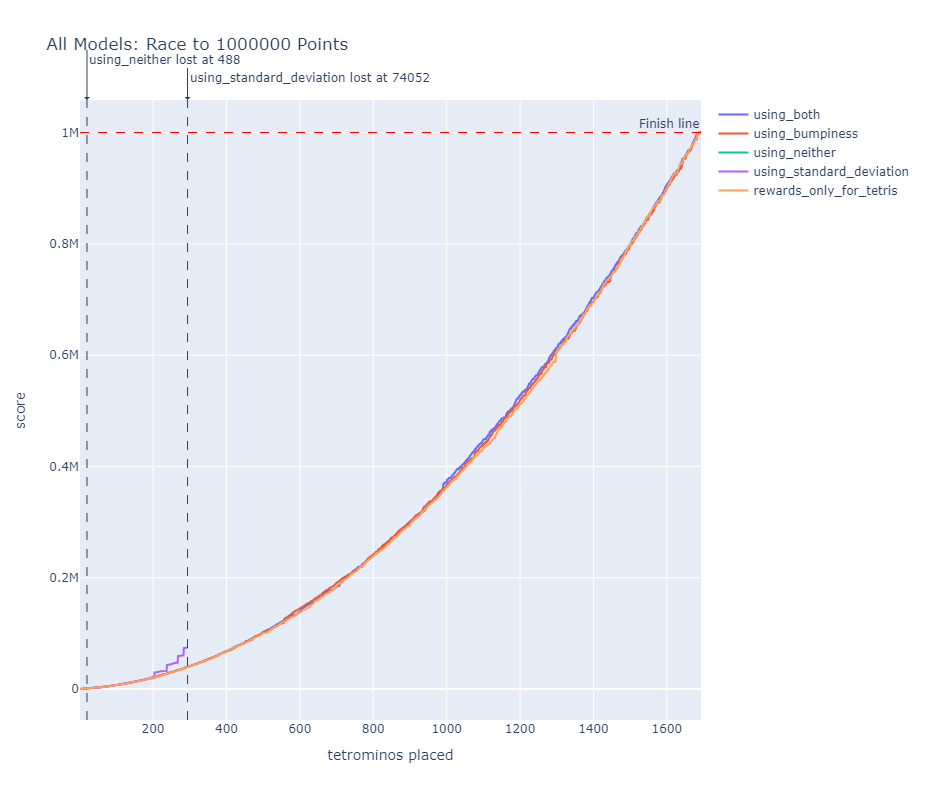
Diese Ergebnisse demonstrieren sowohl die Stärken als auch die Limitierungen des entwickelten Systems: Während die KI erfolgreich stabile, langfristig erfolgreiche Strategien entwickelte, mangelte es ihr an der strategischen Tiefe für komplexere Taktiken wie systematische Tetris-Vorbereitung, die längerfristige Planung über mehrere Züge erfordern würden.

Fazit und Ausblick

Obwohl der entwickelte zweite Lösungsansatz bereits KI-Modelle hervorgebracht hat, die theoretisch unbegrenzt spielen können, existieren vielversprechende Ansätze zur weiteren Leistungssteigerung. Eine naheliegende Erweiterung besteht in der Berücksichtigung des nachfolgenden Tetrominos, der bereits in der Implementierung verfügbar ist. Diese Information könnte den Planungshorizont des Agents erweitern, indem alle möglichen Konstellationen aus aktuellem, gehaltenem und nachfolgendem Tetromino in die Entscheidungsfindung einbezogen werden. Allerdings würde diese Verbesserung die Anzahl zu prüfender Endpositionen exponentiell erhöhen und entsprechend mehr Rechenleistung erfordern.

Ein weiterer vielversprechender Ansatz liegt in der Entwicklung zusätzlicher Features zur State-Repräsentation, die das dominante Bumpiness-Feature ergänzen könnten. Während Bumpiness erfolgreich konservative Strategien fördert, fehlen Features, die kalkulierte Risiken für Bonuspunkte durch mehrfache Reinenräumungen incentivieren. Besonders interessant wäre die Implementierung einer gedanklichen Spielfeldaufteilung, die erfahrene menschliche Spieler anwenden: Die Unterteilung in eine neun Felder breite Stapelzone für lückenloses Ablegen und eine schmale Abbauzone am Rand für strategische Platzierung des I-Tetromino.

Eine alternative Optimierungsstrategie könnte im Vorbefüllen des Replay Buffers mit exemplarischen Spielzügen erfahrener menschlicher Spieler liegen, wodurch der Agent von Beginn an Zugang zu qualitativ hochwertigen Entscheidungsmustern hätte.

Die vorliegende Arbeit hat erfolgreich die praktische Anwendung von Deep Q-Learning auf das komplexe Problem des Tetris-Spielens demonstriert und dabei sowohl die theoretischen Grundlagen als auch die praktischen Herausforderungen des Reinforcement Learning beleuchtet. Der entwickelte Ansatz verdeutlicht eine fundamentale Erkenntnis des maschinellen Lernens: Die präzise Problemdefinition ist oft entscheidender als die algorithmische Raffinesse.

Der Fehlschlag des ersten Lösungsansatzes illustriert eindrucksvoll, wie eine theoretisch korrekte Implementierung an der falschen Problemabstraktion scheitern kann. Obwohl der Agent über dieselben Eingabemöglichkeiten wie ein menschlicher Spieler verfügte, fokussierte er sich auf die Navigation der Tetrominos statt auf die strategische Positionierung. Diese Erkenntnis führte zur fundamentalen Neukonzeption des zweiten Ansatzes, der die menschliche Denkweise erfolgreicher nachahmte, indem er die Schrittweite von atomaren Bewegungen auf komplette Platzierungsentscheidungen erweiterte.

Die notwendige Abweichung vom theoretischen Deep Q-Learning Modell - insbesondere die Verletzung der Prämisse konstanter Aktionsanzahl - erwies sich als pragmatisch richtige Entscheidung. Die Gleichsetzung von Action- und State-Qualität ermöglichte einen flexiblen Vergleich aller erreichbaren Endpositionen und führte zu dem beobachteten Durchbruch in der Lernleistung.

Die umfangreichen Experimente mit verschiedenen Modellvarianten offenbarten die dominante Rolle spezifischer Features bei der Strategieentwicklung. Das Bumpiness-Feature erwies sich als besonders einflussreich und förderte konsistent konservative, risikoarme Spielstile mit stabilen Leistungen, während das Standardabweichungs-Feature aggressivere, aber volatilere Strategien begünstigte. Diese Dichotomie zwischen Sicherheit und Ertragspotential spiegelt fundamentale Entscheidungsdilemmata in vielen realen Anwendungsgebieten wider.

Die zeitlichen Begrenzungen dieser Arbeit verhinderten die Exploration weiterer Optimierungsansätze, doch die geschaffene Grundlage bietet vielfältige Anknüpfungspunkte für zukünftige Forschung. Die entwickelten Modelle demonstrieren eindrucksvoll, wie Deep Q-Learning komplexe strategische Probleme erfolgreich bewältigen kann, wenn die Problemformulierung an die spezifischen Anforderungen der Domäne angepasst wird.